How to recognize a real Mountain?

Everyone has an intuitive sense of what a mountain is – something very large in relation to what surrounds it. This notion is reflected in our speech. I have a mountain of work - huge in relation to my normal workload. He’s a mountain of a man – large in relation to other men. I’m goin’ into the mountains – an uplift which is much taller than the surrounding areas.

As I discovered through experience our sense of mountain is subjective. This discussion is meant to impart some objective criteria to our subjective sense of mountain.

We want an objective way of determining what a mountain is. How can one tell the difference between real and false summits? How can one differentiate true mountain from a poseur. Obviously height is a criterion. But how high does a hill have to be to become a mountain? This is akin to the question how many grains of sand does it take to become a pile? As we shall discover where the line is drawn is personal and subject to popular usage.

How tall is a Mountain?

In discussing the Munros of Scotland Ralph Storer mentions three criteria needed to determine a mountain. One is altitude, two, how much of a dip is needed between two separate mountains, and three, how far away do the mountains have to be from each other. Let us discuss these criteria a bit.

Munro chose the arbitrary number of 3000 ft above sea level as the cutoff point between real mountains and mere peaks. Why he chose 3000 feet is nowhere left for posterity, but we can imagine that it is a nice round number, which separates a majority of the peaks from the mountains rising above. Although the 3000 foot altitude criterion is an effective way of differentiating peaks from mountains in Scotland, elsewhere it has no meaning. For instance the mountains of the Eastern Sierras start at a base of 4000 feet above sea level. In Scotland sea level works well as the base because all mountains in Scotland rise more or less from the ocean. This criterion fails in the Eastern Sierras and on Mars, which has no water.

With these obvious difficulties why are altitudes on the Earth measured from mean sea level?

On the most apparent level it is the easiest and most practical. How high is the land above the water? However that is begging the question. The air pressure is linked to the sea level. The air pressure is linked to how we can breath. Hence practically speaking, the height above sea level conveys how easy it will be to breathe. So independent of highest, lowest, false or real summit, the altitude above sea level conveys the thickness of air and how that will affect the comfort of our body.

“Cold at altitude can usually be overcome by warm clothing but lack of oxygen is less easily combated. Most of us are adapted to a sea-level air pressure of 15 pounds per square inch, which is just enough to push the amount of oxygen we need through the lungs and into the bloodstream. At 10,000 ft the air pressure is only 10 pounds per square inch, and so oxygen intake is reduced by a third; to compensate you have to breathe harder. At 18,000 ft there is only half as much oxygen around and on the summit of Everest there is only about a quarter. Andean and Himalayan peoples have adapted to high altitudes by having more blood in their bodies and larger red blood cells. ...The only strategy available to most of us when climbing high is to take it slowly and acclimatize. Otherwise you will suffer.” (Storer, p14)

As a rule of thumb, at 12,000 feet there is about half as much oxygen around as at sea level. Humans used sea level as the measuring point for practical reasons not technical ones. The intuition was based upon practicality.

Ralph Storer has some other suggestions, which address some of the problems of measuring altitude from sea level.

“After all, would global warming, melting ice caps and rising sea-levels reduce the height of mountains? As we look forward to a future of space travel and intergalactic hillwalking, how will we measure the height of mountains on planets that have no seas. ... Currently lunar and planetary altitudes are measured relative to an adopted reference sphere. This means that for mapping purposes the moon, for example, is regarded as a perfect sphere of radius 1,008 miles (1,738 km), and this is used as the base level for all height measurements, even though the actual surface varies from this by 4 km (a sizable variation when it comes to climbing. ... One universal method of measuring altitude would be to measure the height of a mountain from the bottom of the nearest depression, be it filled with sea water or not.” (Storer, pp. 11-12)

 

Storer has suggested three types of altitude criteria – sea level, from the radius of the planet, and from the nearest depression. This yields vastly different relative altitudes. Measured from sea level Mt. Everest (8848m) is the tallest, but it is only 9000 feet above the adjacent plane. The Argentinean peak Aconcagua (6969m) is not nearly as far above sea level as Mt. Everest but rises 9 miles from the nearby ocean trench to the peak. If we measured altitude by reference to the radius of the sphere like the rest of the planets, then the Ecuadorian volcano Chimborazo (6267m) would be tallest because of the Earth’s irregularities.

It’s obvious that each criteria has problems associated with it. For instance if we were to use the nearest depression to determine height how is this base determined? The idea of base has the same ambiguities associated with it as do peaks. How does one distinguish a real from a false bottom? How does one determine the nearest depression? Where does one draw the line?

This is the main issue. Wherever that line is drawn is subjective. Subjectivity is built into each of the criteria. At the extremes there is no complexity. Mount Everest is a mountain; Miami Beach is a beach. The ambiguities occur in-between, as one approaches the middle – the fractalization of the boundary line. But let us investigate the boundary line by employing Munroe’s 3 mountain criteria.

Distance and Drop and the Eastern Sierras

Storer has illustrated the ambiguities of mountains of Scotland. We have looked at the Santa Ynez Mountains, which contain no mountains. Now let us look at the Eastern Sierras around Onion Valley outside of Independence, California to better understand the last two criteria for determining separate mountains.

Looking at the mountain range from Independence there is no doubt that the Eastern Sierra mountain range rises dramatically from the base. Within this geography the base presents no ambiguities. Onion Valley lies 5000 feet above the valley floor, 9000 feet above sea level. By any reasonable standard this qualifies as a mountain range. Obviously they meet Munroe’s 3000 feet altitude criteria. But is this merely a mountain ridge like the Santa Ynez Mountains or are there real mountains upon it? Hiking up its steep paths, one sees mountains towering high above. As an insignificant ant, one is humbled by the awesome grandeur. There is no paved road on the ridge; nobody hikes or bikes the ridge. There must be some real mountains here if anywhere.

Looking at the topo map of the area, we are delighted to see a Mount Gould (3964m), Black Mountain (4051m), Mount Rixford (3928m), and Mount Bago (3618m). There is also Dragon Peak (3940), Independence Peak (3579m) and Kearsarge Peak (3846m). There are also some unnamed peaks at 3940m, 3912m, 3877m, 3838m, and 3645m.

Uh, oh! Problems. An unnamed peak at 3940m is over 300 meters taller than Mount Bago at 3618m. How, what, when, why, where? How is it that an unnamed peak is taller than a mountain? Looking even closer we notice that there are many named and unnamed peaks that are higher than mountains in the same geographical area. Why? Let us apply our mountain criterion to see what they reveal.

 

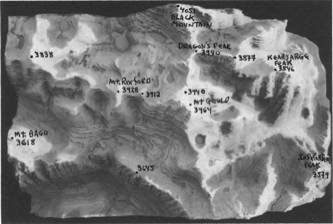
Looking at the topo sculture it is easily apparent that this slice of the East Sierras consists of one ridge extending in a north-south direction (that we will call the Eastern Sierra Ridge), which is intersected by 3 ridges, which extend from east to west. We will refer to the center one as the Kearsarge Ridge. Although Mount Gould and Black Mountain are both part of the Eastern Sierra Ridge they are separated by a pass over 400 meters deep and are approximately a mile from each other. According to the Munro criteria, ‘half a mile separation and an intervening drop of 500 feet’, Mount Gould and Black Mountain would both be considered separate mountains even though they belong to the same ridge.

The Mount Gould mountainous area is at the intersection of the Kearsarge and Eastern Sierra Ridges. The Mt. Gould mountainous area contains the unnamed peak and Dragon Peak, both at 3940m. The unnamed peak is separated from Mt. Gould by a drop of only 60 meters and a distance of only 1000 feet, hence is unworthy of a name even though it rises to a peak over 12,000 above sea level. Dragon Peak is separated from Mount Gould by a drop of 140 meters and a distance of about 4000 feet. Dragon Peak could almost be considered a mountain because the drop is almost 500 feet. Of course the 500 feet cut off point is arbitrary. If we dropped our criterion to 400 feet then Dragon Peak becomes a mountain.

Mt. Rixford at 3928 meters qualifies as a real mountain under the Munro criterion even though it is part of the Kearsarge Ridge, because it is over a mile away from Mt. Gould and is separated by a drop of 200 meters ≈ 650 feet. Another unnamed peak at 3912m is only 2000 feet away from Mount Rixford while a drop of 180 meters ≈ 580 feet separates them. This cute little peak has no name because Mt. Rixford cancels it out.

Although each peak is part of the Kearsarge Ridge, a deep pass separates them. Furthermore they both rise dramatically from the base of the ridge at 3740 m. If we drew our line of separation at 1/3 of a mile apart rather than 1/2 mile, we would have another mountain. Conversely if we drew our line at one and a half miles, Mt. Rixford would become an unnamed peak.

Furthermore if Munro’s drop line was based upon relative height then his intervening drop of 500 feet in mountains of 4000 feet would be about a 12% drop. A 12% drop at 4000 meters is 500 meters or ≈ 1600 feet. Scratch Mt. Rixford and Mount Gould as both are smaller than Black Mountain and are not separated by a pass or valley of 500 meters.

Note: in the Scottish Highlands, valleys separate mountains. Similarly long erosional valleys separate our local mountains in the San Rafael Range. Alternately passes separate mountains in the Eastern Sierras. The many passes of the Eastern Sierras reflects the ridge like nature of the mountainous configuration there. One tries to find a depression in the ridge, called a pass, to cross over to the basin on the other side. This is why a closed pass can totally limit access to a particular area in the Eastern Sierras.

The Perspective of a 60,000 Giant
or an Example of Relative Drop

One of our family discussions illustrates the notion of relative drop. We were looking at my topo sculpture - the 3 dimensional representation of the mountains of Onion Valley and Kiersarge Pass that we have been discussing. Note 20 meters (≈ 66 feet) in altitude is represented by a layer of 1/16 “ foam core on our topography map; 1/200” on our map represents a height of approximately 5 feet. Hence if we put a scale model human on our topography sculpture, he would only be 1/10 of a millimeter high. Or conversely a 5-foot child would be 10,000 times taller than our scale human - over 60,000 feet tall – more than double the size of Mount Everest. With this perspective in mind I posed some questions.

I asked Miranda, my youngest daughter, which were mountains from her perspective as a relative giant.

From her giant perspective she responded quizzically, “Do you mean which is the mountain or which are the mountain peaks?”

“What do you mean?”

“Well the whole thing is the mountain with a whole bunch of peaks.”

“Is Mt. Gould the mountain?”

“No way! It is just a small part of the mountain.”

I then asked my wife and Serena, my oldest daughter, the same question. In attempting to understand what I was asking their answers were equally perplexing,.

My wife, after her Santa Ynez mountain experience, said, “It’s just like the Santa Ynez Mountains - except that the mountain is a series of intersecting ridges instead of just one ridge. It is a mountain range with no individual mountains, only peaks.”

Indeed from the giant’s perspective we see no individual mountains only a few peaks upon the collective mountain range. However from the position of puny ant crawling over the huge expanse, we only see huge peaks towering above us. Mt. Rixford is the tallest peak in one region, while Mt. Gould is the tallest in another. From our giant perspective, these towering peaks are only part of a greater ridge. As a giant a mere 500-foot drop between peaks is really very little and doesn’t impress us as mountain. Because we see a 8000 foot rise from valley floor to mountain top Munroe’s 500 foot drop criteria is insignificant. However a 500 meter drop between peaks would be enough for us to perceive individual mountains rather than ridges with peaks. This relativity of perception indicates the importance of personal viewpoint in the determination of mountains. Let’s apply this insight.

Why isn’t Kearsarge Peak a Mountain?
or the Trail Criteria

Kearsarge Peak at 3846m is a continuation of the Kearsarge Ridge towards the east, past the Eastern Sierra Ridge, projecting into the valley. It is almost 2 miles from the nearest mountain, Mt. Gould, and a drop of 200m separates the two. It is the tallest peak within over a half-mile radius. It exceeds all the same criteria that made Mt. Rixford a mountain. Why is it not a mountain?

When looking at the mountain ridge from the valley below one sees mountains behind Kearsarge Peak. Even though from one’s puny perspective one can’t tell how far away it is from Mount Gould, Mount Gould does tower above it. When hiking the trail along the Kearsarge Ridge, one looks up at Mt. Rixford and sees Mt. Gould in the distance. Because of perspective one sees two distinct mountains.

Here we have the mountain determined by the perspective of the trail. Kearsarge Peak becomes only a peak because the trail perspective shows a higher mountain behind it, while Mt. Rixford is a mountain because from the trail, which moves parallel to the Kearsarge Ridge, there is no mountain visually behind it. Although from our giant’s perspective Mt. Rixford is no more or less a mountain than is Kearsarge Peak, human’s naming mountains were denied this view. Thus in this case the geography of the region determined the visuals, which determined mountainness. We now have another criterion. If there is a mountain towering behind a summit, then it is only a peak, no matter how tall it is. Conversely if one can’t see anything taller behind it from the trail, it has a better chance of being called mountain.

Classic Peaks

Independence Peak at 3579m and the tallest peak in Kearsarge Pinnacles at 3645m, which is unnamed, are classic peaks from the above definition. Although relative summits of their respective ridges, they rise only 80 meters above the base. Additionally from the paths, they are surpassed visually by taller mountains in the immediate vicinity.

Our two other unnamed peaks at 3877m and 3838m we will analyze visually. The 3877m peak has two problems. Although it is taller than Kearsarge Peak, it is immediately behind it and can’t be seen from our puny human perspective. Secondly it is visually part of a ridge - not a peak. Third when it comes into view so does Mt. Gould. As a human there was no gut reaction to name it because it is overshadowed visually first by Kearsarge Peak and then by Mt. Gould.

The other unnamed peak at 3838m is over a mile west of Mt. Rixford and over a mile east of Mt. Gardiner on the Kearsarge Ridge. It is separated by a drop of 160 meters (over 500 feet) from either mountain. It is visually distinct with no mountain overshadowing it in either direction. By current criteria, a mountain. But it is unnamed, not even graced by the name peak. Why?

It doesn’t rise rapidly enough to a summit to be named a mountain or peak. The rise of the 2000-foot ridge, which starts at 3800 meters, is very shallow, relatively speaking. We now have another criteria to deal with, the angle of the rise. How large does the angle of the rise have to be for the summit to be considered a peak? Conversely how big does it have to be to be considered a ridge. Where is this line drawn? Obviously in this case a 2000 foot ridge doesn’t yield a nameable peak, especially when it contains three mini peaks, not one.

Why is Mt. Bago a Mountain?

Mt. Bago at 3618 meters is over 200 meters ≈ 660 feet smaller than the aforementioned unnamed ridge. It is a bit over a mile south of the ridge and is separated from it by a drop of about 500 meters. Visually the paths go between the two projections. Mt. Bago is never overshadowed by the unnamed mini ridge. On the ridge side there is a drop of 500 meters ≈ 2000 feet; on the other side there is a drop of 1100 meters ≈ 4000 feet. This is a mountain in anyone’s book. Or is it?

A natural upward projection from a base of 4000 feet, Mt. Bago is an imposing piece of geography, physically and visually, especially if you are a puny human looking up at it from your normal human perspective - a path. It is definitely a mountain from the human perspective. However if you are a 60,000 foot giant looking down upon it, Mount Bago is a mere peak in the Eastern Sierra Mountain Range. Why is this?

We giants draw our lines in different places. Although Mt. Bago is over 3 miles from Mt. Gould, and almost 2 miles from the Kearsarge Ridge. For we giants an inch is less than 1/2 a mile. We are looking at a mountain range over 200 miles long by over 50 miles wide. With this context, 3 miles is nothing. On a planetary perspective Mount Bago would barely register as a small bump. From our giant perspective we might choose to draw our relative line between mountains at 5 or 10 miles. Then Mount Bago evaporates into a mere peak.

The Inherent Ambiguity of Words

Where we decide to draw the line determines the filter through which we view the world. One side of the line we call mountain, the other side we call hill. One side we call peak the other side is the true summit. Where we draw the line has no scientific basis, it is purely subjective, although geographers may have established a technical convention, which more or less matches popular conceptions. A slight shift in the line might destroy or create mountains depending on which way the line is shifted.

In some ways this paper is about the ambiguities of definition and word, a topic dear to my heart. Hence for our idealized mountain, there is the reality of the world. Thus although we have an instinctive notion of what a mountain is, how do we apply it? Pattern Recognition. We humans have it. How do you program it into a computer? Although we all have an instinctive notion of what a mountain is we are looking for some absolute criteria to plug into our imaginary computer so that it can analyze a topography map of the earth to determine which are mere hills and which are true mountains, not just impostors posing as mountains. What is the mountain pattern?

This essay is in no way meant to attack conventional language nor is it meant to establish any technical knowledge. Instead it is an attempt to understand the intuitive logic behind the word mountain. We humans intuitively know what we mean by mountain. How do we apply logic to this intuitive sense? What do we objectively mean when we say mountain. That boundaries blur into a continuum is part of the thrust. But this paper also attempts to understand the language of mountains. We discovered why Montecito Peak and La Cumbre Peak are not mountains, when there are Scottish mountains shorter than them? We’ve also seen why there are no mountains in the Santa Ynez Mountain Range? Rather than attacking the words we are trying to understand the human meaning behind them.

Language wants to communicate. In the British Isles with all their rolling plains, language wants to express the difference between the rolling hills and the peaks, which rise above them. It calls the high peaks mountains - the superstars of hills. Those in the Kentucky hills say that they live up on the mountain to distinguish it from the valley or the small rolling hills below. Perhaps upon the topography map these ‘mountains’ are referred to as peaks or not even named. But to the people living there, they live on their own mountains. The word ‘mountain’ is a relative term not absolute.

While language needs to communicate, it also wants to be precise. This is what we were trying to pin down. We saw that while mountains have the three parameters of altitude, distance,and drop, that each of these criterion are also relative. Those of us with a technical bent want everything precisely pinned down and delineated. We derisively call the amorphous land of intuition ‘women’s logic’.

Traditional logic is based upon the basic premise that it either is or isn’t. This is deductive logic. What we’ll call women’s logic or intuitive logic is based upon the inclusive idea of ‘both-and’. Deductive logic is based upon exclusion; while intuitional logic is based upon inclusion. The borders with traditional logic are crystal clear, totally precise, and without ambiguity. In intuitive logic there are no borders, only continuums with arbitrary boundaries. Of course the ‘women’s logic’ including everything, holds onto boundaries when necessary and lets them go when feeling the need. In this essay the writer is given a persona with traditional logic. So he has the tendency to chide the silliness of his wife when she talks about joining the mountain category as a group. While the intuitive sense of mountain that she has, is what we’re trying to blend with the absolutes of the technical world. We are not trying to learn who is right. Rather we are trying to learn how they are both right.

The world of ‘women’s logic’ consists of lists of qualifications rather than a few absolutes. We men like things simple. Thus we have Munro’s height limit of 3000 feet, when in actuality we’ve seen that a mountain is an intuitive concept. It is easily defined as a natural projection that rises far above its base, with nothing as big around it. However we’ve seen in many examples that where the lines are drawn is relative to the observer, rather than set by some absolute truth.