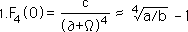
Home Science Page Data Stream Momentum Directionals Root Beings The Experiment
We have just seen how mathematics can be treated as an experimental science. Further we saw how our particular brand of iterative equations is self-correcting, lucky for us. Now let us move into our study of Stressed out Equations, which we discovered in the midst of our mathematical experimentation. Let us begin with the history.
After a long struggle to find an equation to simply express all rational roots, we discovered a whole class of equations, which seemed to also yield the desired Root. These iterative equations were distinct from our General Root Equation and yet similar to it.
Before burning all of our papers. We decided to do some experimentation. The first examples of the Root Number that we tried were the simplest, i.e., 2, 3, 1/2. A strange assortment of equations all worked just fine, as we shall soon see. However when we tried some larger numbers our equations fell apart. These equations we will call the Bogus Equations, because they work under ‘Normal’ circumstances, while falling apart under pressure.
This was just one more case of the experimental reality being much different than mental preconceptions. We thought that there would be only one equation that would work. In most situations that we’ve encountered only one equation works, the rest are wrong. The second misconception was that if an equation is right, it is always right. On math tests, it is right or wrong, not right under certain circumstances and wrong under others. If one has ever dealt with data, one finds that one’s mental conclusions are mostly wrong. But finding these mental stretches in the world of abstract numbers certainly made the top of our heads tingle.
As an experimenter, we wanted to discover under which circumstances these other equations worked and didn’t work to get the desired result. For clarity we defined ‘Normal Circumstances’ as any Root Number that will eventually lead a specific Bogus Equation to the specified Root. We defined ‘Exceptional Circumstance’ as any Root Number that will not lead a specific Bogus Equation to the Root. Some Root Numbers are ‘Normal’ for certain Bogus Equations and ‘Exceptional’ for other Bogus Equations.
Before getting into any analysis let us speak a little about the language to come. We believe in the interconnectedness of all things. Although in reality we are only speaking about the simple foundation of dry numbers, our language wants to link it to the Quest for the Holy Grail.
In our minds we think of these different iterative equations each with their own personality. We will call them Root Beings. These little equations are not just stay at home equations. They are going somewhere. With each iteration they are moving into the future, away from the past. We will speak of each iteration as a moment in time. We will view the elements of the F&D Series as a continuous time sequence.
Our Root Beings are Born, F(1), from Nothing, F(0), and immediately begin seeking perfection, their impossible goal, F(į), the True Root, their Destiny. These equations move forward in time with each iteration. They are ardently seeking to fulfill their Destiny, which they will never reach. Their existence is bound up with this endless quest for perfection.
No matter where our Root Beings are born, they always head inexorably towards their Destiny. Their initial starting point, (as long as it is not all zeros for the D Series), has no effect upon the Root. Birthplace has no effect on their Destiny. This is like the Seed, which yields the same plant no matter where it is planted.
We will refer to each of the iterations as an Event. We will refer to the Nth iteration of the F or D Series, ń(N) or d(N), as the Present Event or the Now, as represented by the notation F(0) and D(0). We will refer to ń(N-1), i.e. F(1), or d(N-1), i.e. D(1) as the Past Event. When we say, the Past Three Events, we mean ń(N-1), ń(N-2), ń(N-3), i.e., F(1), F(2), F(3), or d(N-1), d(N-2), d(N-3), i.e., D(1), D(2), D(3). Just after it is born refers to the first few events after its birth, perhaps d(1), d(2), and d(3). Just as we have Past Events, we also have Future Events that will occur after the Present Event. Mind that this time sequence is purely projective.
We view the F&D Series just like we do Living Data Streams. Once these series are born they never really die. Each is totally built upon contextual data. Each is continually changing. They both have incredible integrity, in the sense of being incredibly stabilized by the Past. Further both have a Pattern that they follow religiously. Also each element of both series is a function of all the past elements.
One big difference between our Living Data Streams and our F&D Series is that fresh data is always fed into the Living Data Streams while the F&D Series are fed upon themselves. Because no outside elements are fed into the F&D Series, the Root Beings generated by them move in distinct and preordained ways. Their lives are predestined. Each has a distinct pattern that is always followed. We'll call it the Pattern. Each Root Being has the Pattern set with Birth; it is never-changing and always leads these Root Beings towards their Destiny, the True Root, impossibly striving, never reaching, tragically moving forward against all odds.
In contrast the Living Data Streams, because they are always fed with ‘fresh’ data, have an undetermined goal. Their life is in no ways predetermined. This is why we call them ‘Living’ Data Streams as opposed to ‘Dead’ Data Streams. While our Root Beings have a lots of personality, as we shall explore, they are indeed Dead Data Streams because their fate of is predetermined.
While each of our Root Beings has a predetermined Fate, it is not always the same. It differs depending upon the Circumstances thrown at them. While each Root Being has a unique Pattern, these Patterns have differing abilities of dealing with the different Numbers, a/b, which they are seeking the Root of. As we will see, Normal circumstances circle around 1, while Exceptional Circumstance begin above about 10 or 20 depending upon our Root Being. Under Normal Circumstances most of our Root Beings will move inexorably towards the Root, while under Exceptional Circumstances only one of the Root Beings will stay on course. The rest of the Root Beings either fall apart, dissipate or seek an Undefined Root.
Finally our Root Beings are always seeking to perfect themselves, refining themselves with each new event. Purifying, refining, mixing and blending. Always using the refinements to make more refinements. They use the lessons they have learned to further perfect themselves in the pursuit of their Destiny.
Anyway my little Root Beings have a lot of personality. However they are a little stuck up because they feel that they have a Mission in life, while most equations just sit there, going nowhere. My Root Beings are multiple level feedback equations while most equations are zero level feedback equations.
Many of our Root Beings will approach their Destiny, the True Root, under Normal Circumstances. However only one of the Root Beings of each Dimensional order will continue to approach the Root under Exceptional Circumstances. We call this the True Root Being. The equations, or Root Beings, which don’t perform well under Exceptional Circumstances, we will call Stressed out Equations. Remember they only get tweaked or stressed out under Exceptional Circumstances; under Normal Circumstances they perform just fine.
What do we mean by Normal Circumstances? First what are Circumstances? As we mentioned each Root Being has a different Pattern. This Pattern, when iterated, is supposed to yield successively closer approximations to the True Root of any Number. The Number, whose Root is sought, is the Circumstance of the Root Being. All the numbers represent all of the Circumstances for our Root Beings. Our Root Beings behave differently under different Circumstances. Sometimes they behave well, i.e. continuing to pursue their Destiny, the True Root. Other times they don’t behave, i.e. they lose touch with their Destiny, the true Root. When they behave, it is called Normal Circumstances; when they don’t behave, it is called Exceptional Circumstances. Now that you, the Reader, know a little more about our Root Beings, it will be easier to get acquainted.
Now that we have introduced the Reader to the language of Root Beings, let us speak about the Seeds of our Root Beings. In the process we will differentiate between ‘ordinary’ and ‘inverted’ dimensionality, context and content, Pattern and Number.
The seed of our iterative equation is its point of origin. This is another parallel between regular dimensions and the inverted dimensions of our Root Equations. The point of origin for a line has only one coordinate. The point of origin for a plane has two coordinates, while the point of origin for three dimensions has three coordinates, and so forth. This parallels our inverted dimensions, if one views the seed as the point of origin for our inverted dimensions. For the square root the F Series needs only one coordinate, while for the cube root two coordinates are needed, and for the fourth root three coordinates are needed. If a closer parallel is needed, the D Series needs as many coordinates as their are Roots. Hence the 7th Root needs 7 coordinates, or seed positions, to even begin the Series.
This connects the Roots in one other context with dimensionality. The Point of Origin of regular dimensionality has to do with a point in space, while the point of origin of inverted dimensionality has to do with the number of contextual elements needed to generate the next. While the elements of regular dimensionality are defined by their relation or distance from the point of origin, with inverted dimensionality each element is defined as a specific function of the number of the Root. Our Roots are contextual numbers while our regular numbers are content-based numbers. Because our Root Beings are contextual patterns their Point of Origin, their seed, has no effect on their Destiny, where they are going.
Because Regular Numbers are based upon content, the Point of Origin is all determining as to their name. Regular whole numbers are going nowhere. They just are. Fractional decimals approach their goal steadily linearly from below by adding on. There are no Root Decimals, period. Our Root Beings approximate all Whole Numbers, all rational numbers and all rational roots, the same way, as we shall see, globally consistent, locally erratic.
Enough verbiage, let us be a little more specific. The thrust of this paper is to differentiate between the True and Bogus Equations. In this paper we will focus only upon 4th order Root Beings, interesting but not too complex. Let us begin with some algebra so that we can easily name our Beings in a consistent manner.
Following is the General F Series Equation for the 4th Root.
Below is the expansion.
This equation, for this discussion, can also be represented as three ordered pairs, (shown above). The first number is the binomial coefficient while the second number is the element of the F Series. This sequence of three ordered pairs is the True Equation. As we shall see each of these numbers must be precise for it to be the True Equation.
Below are the General Root Formula for the one True and all Bogus Equations of the 4th order.
When A, B, and C are positive integers the above iterative equation will approach the Root when our Root Number is Normal, as defined above. Here are some specific examples of Bogus Equations with their numerical representations.
Here are some other examples of Bogus Equations that we explored.
Note that all of the Bogus Equations retain the binomial coefficients for the first numbers of the ordered pairs. Through experimentation it was established, beyond a reasonable doubt, that these coefficients are invariable if the Root is sought. It seems that all Bogus Equations have these coefficients, or a multiple thereof. (Remember that Bogus Equations work under Normal Circumstances.)
Below is a general representation of all equations of 4th order. These are equations which iterate like the 4th root, i.e. employing any past three values of the series to compute the next, executed in the following manner.
We call this the General 4th Order Root Equation. Only when D, E, & G equal 4, 6, & 4 respectively, i.e. the binomial coefficients, are they called Bogus Equations. If it is in the Bogus Equation family and A, B, & C equal 1, 2, & 3 respectively it is the True Equation.
If D, E, & G equal anything other than 4, 6, & 4, then it is a False Equation, i.e. while approaching something, it does not approach the True Root. Here is one example of an False Root Equation of the 4th order.
Note that A, B, & C equal 1, 2, & 3, like in the True Equation. Also D and E are equal to 4 and 6 just like in the True Equation. Only the coefficient G is off by just one. G equals three instead of four. However the Root that this iterative equation approaches is close to but distinctly different from the True Root. Although it is not the True Root, it does belong to the 4th order of Root Equations. Its limit is real while not expressible as the root of any rational number. (This last statement is an unproved intuitive guess only.)