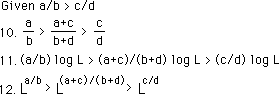
Home Science Page Data Stream Momentum Directionals Root Beings The Experiment
Now that we understand how the Mandelbrot set is organized geometrically, let us see how this organization is connected with the System of our Root Beings.
First we need to establish the connection between the F Series of the Root Beings and the In-between Fractions.
We just proved and demonstrated a process whereby two fractions are merged to create an in-between fraction, which we’ve referred to as The Process. This same process applies to the values of fractional roots. (This proof follows in step numbers from the previous proof.)
We know equation 10 to be true because of the In-between Fraction Theorem. In step 11 we multiply all parts of the inequality by log L, where L represents any rational number greater than 1. Therefore log L is positive and won't change the direction of the inequalities. We then raise all parts of the inequality to being the exponent of 10. 10 raised to log L equals L. This yields step 12. Similarly if L is between 0 and 1 the same process would apply but all of the inequality signs would be reversed but still the middle expression stays in-between. This only proves that the rational roots order themselves numerically in a similar way to rational numbers. This is an important theorem for what follows.
Below is the In-between Root Theorem, which we shall be leaning upon. Remember that a, b, c, & d are all positive integers.
Note that the in-between expression is in the middle no matter if L is above or below one. We will see that one divides Exponent Land in half just as zero divides the real number line into negative and positive.
We are getting close to connecting up with the Root Beings and their F Series. Before moving on let us remember some of the Givens and Provens from the preceding Notebooks.
The first equation is the General Binomialized Root Formula, Theorem 1. The second represents the Limit as the number of iterations approach infinity. The third represents the value of our constant c, generalized to include any fractional root.
In step 13 we just restate the Givens above with the new notation to remind ourselves that the iterated F Series only approximates the Root minus one, while F to the Root power is the infinite limit.
We are ready for our In-between F Series Theorem. Let L replace a/b as a positive rational number in the above Givens and Provens. Because of the inequalities we will let L be a rational number greater than one. To avoid confusion we will use M, N, P, Q as the positive integers, with M/N>P/Q as a given.
Because of the givens we know that the first expression of the In-between Root Theorem is true. We subtract one from each expression in this theorem to obtain Step 14. Using the definitional equation of Step 13 we arrive at Step 15. This is the relation that we were trying to prove. Again if L is between 0 and 1 then the same reasoning holds except that the inequality signs are reversed.
Now we are ready to state our In-between F Series Theorem.
This theorem only states that the F Series orders itself in the same way as the rational roots which order themselves by a similar process as rational numbers. Notice that the in-between F Series is in the middle no matter which condition.
The following section shows the F Series representation of the In-between Root.
Step 16 only illustrates that the inequality between the finite F Series representation is approximate and becomes exact as the number of iterations approaches infinity. Steps 17 and 18 merely restates these finite F Series in terms of the exponents, M/N and P/Q, and the Root Number, L, instead of the constant c. Step 19 shows the in-between fractional root of the same rational number.
We’ve seen that fractions, rational roots, the F Series, and the Mandelbrot set all organize themselves in a similar fashion. They all rely upon the In-between Process to find the In-between Fraction, whether for rational numbers, fractional roots, or the period of the Mandelbrot bulbs. In this section we are going to attempt to come to a greater understanding of the In-between Root, by understanding what it is not.
In attempting to understand what the In-between Root is, we are tempted to equate it with the product of the F series tied to the appropriate Roots. The F Series Product tantalizes us with similarities to the In-between Root. Let us take a look.
The left equality is based upon the derived definitional formulas for the F Series. The right equality is based upon the expression that we just derived for the In-between Root. In the extended inequality we see why they are not the same.
It seems easy enough to just multiply the second expression through to get the third expression. Seems simple enough algebra, which it is. However our infinitesimals and dimensionals are not real numbers. The exponent of our infinitesimal expression while indicating a type of binomial expansion does not add like normal exponents. Hence the simple multiplication does not work. We will return to this idea in more detail in a little bit.
Further even if these numbers were normal the middle expression does not yield the right equality either. It yields a few extra terms. These simple multiplications are close to our In-between Fraction but don’t yield any prizes yet. Thus while our In-between Root has an incredible similarity to the supposed product of the F expressions, neither the product is true or the connection between the two. This is the first thing that the In-between Root is not, the Product of F Series.
The product of the F Series is not the In-between Root nor is the product of the Roots. Previously we proved that the Rational Roots have the same relation to each other as do the equivalent F Series. This is shown in step 1, below.
This is because the limit of the F Series ‘+ 1’ equals the Rational Root. This ‘+ 1’ does nothing to change the relative size with regards each other. However this ‘+ 1’ changes the products significantly. Therefore in no way does the product of the Roots equal or approximate the Product of the F Series. This is stated in step 2.
Let us also introduce a notational shortcut that we will use soon.
Stated simply, F raised to an exponent is the infinite limit of the iterated series. This leads to the following expression.
The first part of the equality is F Series Theorem. The second part is the simplified notation.
Below is shown the product of two fractional roots as seen through the F Series. L, as before, represents any positive rational number. Each of these expressions represents a real number so we can treat the expansion with the normal algebraic procedures.
In step 3 we show the expression for the Product of the Rational Root Parents in its equivalent F Series expression. In step 4, we expand the expression by multiplying through. In step 5 we show that the difference between the Rational Root Product and the F Series product is the sum of three numbers. In step 6 we show an intriguing equivalence that combines Rational Roots and F Series in a concise fashion.
Below is the simple geometric representation of this process.
We have seen that the Product of the F Series is not the In-between Root, though it is similar, nor is it the Product of Roots, though contained within it. In this section we will reexamine the Process, its parallels and differences with ‘normal’ fraction manipulation.
First let us remember The Process. Add the numerators and denominators of the two parent fractions to yield the in-between child fraction. We math people laugh at this technique for ordinary fractions because we know that for equalities we need the precision of common denominators for the combination of numerators. We all know how messy the common denominator stuff can get, especially algebraically. Thus we laugh a little at this elementary technique for dealing with fractions, realizing that it only works with inequalities, not with real equations.
Thus with surprise we introduce a situation where the numerators and denominators of a fraction are added appropriately in a mathematical operation. When multiplying two fractions, nothing is added, just multiplied. However when two identical fractions with different exponents in the numerator and denominator are multiplied, the answer is simply the same fraction with the exponents of the numerators and denominators of the parent fractions added. Shown below.
This is the situation that we have with our Binomialized F Series representation of fractional Roots. Ironically or unusually or incredibly, the F Series representation of Fractional Roots only contains the numerator of the fractional root as an exponent in the numerator of its representation fractional representation. Further, in parallel fashion, the denominator of the fractional root appears only as the exponent in the denominator in the F Series fractional representation. Shown below.
“Why, of course”, the Reader might think. “What’s so unusual about that?” For one, fractional roots do not behave and are never treated is such a fashion with ordinary numbers. For instance the 2/5 root of 7/3 has no relation whatsoever to 7 squared divided by 3 to the fifth power.
This is shown below in the general case.
While for the F Series the Root Number, 7/3, squared minus one, the quantity, divided by an iterative expression raised to the fifth power plus one does equal the aforementioned Root as a Limit. Strange eh!?
Further to find an In-between Rational Root of the same number we need only ‘multiply’ * the two rational roots by each other combining the numerators and denominators as if multiplying common numbers with different exponents. In specifics, we see the process below. The root between the 3/4 and 2/5 roots is the 5/9 root, shown in its manifestation below.
*This is certainly not traditional multiplication, nor does it pretend to be.
In the next two sections, in order to come to a deeper understanding of what the In-between Root represents we are going to derive some theorems that will relate it to more familiar values.
The in-between root fraction above seems almost like the product of the two parent root fractions, but is not quite. Shown below is the algebra differentiating the two.
The above algebraic representation reveals the complexity of the inequality, between the Product Root and the In-between Root. For one major instance, one is the N*Q root while the other is the N+Q Root.
For ease of reference we will refer to these four values as a Family. Note that they all have the same Root Number, i.e. a/b, sometimes called L, any positive rational number. Metaphorically this represents their common genetics, being of the same family. If (a/b)M/N > (a/b)P/Q, then the first is called Hi and second is called Lo. These are the Parent Roots or simply the Parents. The Product of the Parents, called Prod for short, is formed when the Parents join in multiplication. He is the son. The In-between Product, called Mid for short, is formed when the Parents join in the Process, described above. She is the Daughter. These are the two children, i.e. the Kids. This entire section explores the relations between the members of the family. Let us start with the relation between the Kids. In order to understand the Kids let us learn a little about the relation between their exponents.
In order to compare their relative values we would like to break our fractions apart. Therefore we need another theorem. The top equation is the algebraic identity that we will prove.
Simply speaking in step 1 we combine fractional terms in the traditional manner by finding a common denominator and multiplying the numerators by the lacking factors. In step 2 we combine all three fractions with a common denominator. Step 3 we multiply through using the distributive property, also rearranging terms. Step 4 the +BC and -BC in the numerator add to zero. Also we factor an A out of the remaining terms. In Step 5 the A factor in the numerator and denominator cancel out leaving us with the expression on the left side of the equation. This proves our theorem, which we call the extracting a negative from a positive theorem. Shown below.
Now we have the tools to examine the relation between the exponents of the Product Root and the exponents of the In-between Root. Let us prove that the Exponents of the Product Root are greater. The Exponents of the Product Root are on the left, while the exponents of the In-between Root are on the right of the inequality.
In step one we break apart the right fraction apart according to the technique of the Negative from Positive Theorem. Step 2: we employ this theorem again, this time on the second of the three resulting expressions from Step 1. Step 3 we just separate the negative and positive expressions. Because M, N, P, & Q are all positive integers the expression inside the negative parentheses is positive, i.e. greater than zero. This relation is shown in step 4. Because the first two expressions on the right are identical to those on the left and the only expression remaining is negative we know that the expression on the left is greater than the expression on the right, Step 5. This proves our theorem, stated below.
We have just seen that the exponent for the Product Root is greater than the exponent for the In-between Root. How does this effect the relation between the Product Root and the In-between Root? For simplification we re-introduce the Family variables, the Parents, Hi & Lo, and the Kids, Prod & Mid. We spoke about this Family in the introduction to this section.
In steps one and two below we merely state symbolically that the exponent of the Product Root is the quantity, Greater, and that the exponent of the In-between Root is the quantity, Lesser. Step 3 just reiterates our question, i.e. what is the relation between the two roots? Step 4 just represents this relation symbolically.
In Step 5 we divide through by the right side of the equation, which is not negative or zero. In step 6 we just subtract exponents in the normal algebraic fashion, i.e. multiplying top and bottom by L to the negative ‘Lesser’ and then combining exponents. In Step 7 we just mention, in simpler terms, that because the exponent of the Product Root is greater than the In-between exponent, (which was proved in the Sum of Fractions Theorem listed above), that the difference is greater than 0.
In Step 8, L, the Root Number is shown to have an exponent ‘>0’ with some unknown relation to one, which reflects the inequality between the Product and the In-between Roots from Step 3. In step 8A, Both sides of the equation are raised to the inverse of the positive exponent, >0, of step 8. ‘1’ raised to any exponent is always ‘1’. We find that the Root Number, L, has the same relation to 1 as does L raised to a positive power. Steps 9 and 10 point out symbolically that if L the Root Number is greater than 1 then raising it to an exponent ‘>0’ will only make it greater than it was. If this relation is true then we know that the Product Root is always greater than the In-between Root, harking back to the relation of Step 3, when the Root Number is greater than one. Steps 11 and 12 show the situation when the Root Number is less than one, L<1. When a number less than one is raised to a positive exponent, it might be increased or decreased but it will always be less than one and greater than zero. This shows that if a positive Number less than 1 is raised to positive exponent the result will always be less than one. Therefore the Product Root will always be less than the In-between Root, Mid, if the Root Number is less than 1. This leads to the following theorem.
This is the first of a series of In-between Root Theorems. This theorem connects the relative value of the Kids, i.e. Prod & Mid, with their Genetics, i.e. L, the Root Number
The point is that the In-between Root always hugs the middle, the balance point, between the Parent Roots while the Product Root can be anywhere in relation to his Parents, i.e. much greater, much less than or in-between. The In-between Root is much more stable while the Product Root is much less predictable. His Parents have much less effect upon his behavior.
What is the algebraic relation between the Product Root and the In-between Root? In step 1 we reiterate an intermediate result, step 5, in the preceding proof that the Product Exponent is always greater than In-between Exponent. We derived this expression by opening up the expression on the left. This is the exponent for the Root Number, L, to turn it into the In-between Root, Mid. This is shown in step 2. In Step 3 the negative part of the exponent is taken below the horizon as is normal in algebraic affairs.
In step 4 below we evaluate the denominator of Equation 3 separately, giving a common denominator to the exponent by turning the numerator into the sum of fractions. In Step 4A, we first take the denominator of the exponent out of the expression to take a common root of the whole inner expression. This resulting inner expression was noticed to have a sum in the exponent. In Step 4B, this expression was turned into a product in exponential fashion under a common root, N+Q. It was then noticed that this inner product had some familiar friends, L to the P/Q, i.e. Lo, and L to the M/N, i.e. Hi, imbedded in these expressions. In Step 4C, these individuals were raised to the appropriate powers to satisfy the algebraic equality.
Step 4 is the denominator of step 3. These results are written in Step 5. L to the P/Q equals Lo, the smaller Parent Root; L to the M/N equals Hi, the larger Parent Root. In step 6, we make these substitutions for simplification. The numerator is simply Hi*Lo, shown below. The inner product in the denominator is simply Hi raised to the Q power and Lo raised to the N power, this whole product then taken to the N+Q root. This process gives us step 6. A big step.
Remembering that Hi*Lo equals the Product, we substitute this expression into our equation, Step 7. Step 8 reveals the ratio between the Product Root and the In-between Root. This is our answer.
Steps 9 and 10, merely rearrange equation 8. In step 9, we express the equality in terms of the Product Root rather than the In-between Root, Mid. In step 10 we merely acknowledge that the In-between Root has the same root, N+Q, as do Hi and Lo. Thus we put them under a common root roof.
Below is the Theorem that we set out to discover. It is simply Equation 8. This is the Second In-between Root Theorem. It shows the relation between the Kids and the Parents through a simple ratio. The Parents are on the right, while the Children are on the left.
The First In-between Root Theorem established that the Root Product could vary widely in relative size to its Parents, the Hi and Lo Root, while the In-between Root had to be always be in-between. The 2nd Theorem establishes the exact relation between the two. If the expression on the right is greater than one then the Product Root is greater, while if it is less than one then the In-between Root is greater. It will always be greater than one if the Root Number L is greater than one, while it will always be less than one if L is less than one. This merely confirms the results of the first In-between Theorem.
While the past section dealt with the relation of the Product Root to the In-between Root, this section will deal with the In-between Root’s relation to other quantities. Let us start with her relation to her Parent Roots.
Our Parent Roots, called the Hi Root and the Lo Root, had two children, the Product Root and the In-between Root. Last section we explored the relation between the two children. Above is the derivation of the ratio of the Product Root to the In-between Root. Below we derive the relation between the In-between Root and its Parents. We start with equation 6 from the above proof. To simplify this expression we break the whole fraction into two, with the Hi’s on one side and the Lo’s on the other, Step 12.
In Step 13 we multiply the appropriate negative exponents times both the top and bottom of the fractions. This expression is simplified in step 14. Step 15 is the same as step 14, just written in a different form. we see the inner product under the common root of N+Q. This is what we were seeking, the relation between the Hi Root and Lo Root and the In-between Root.
This is stated in the theorem below. This relates the In-between Root to her Parents.
Notice that the exponents of Hi and Low are always less than one because the denominator is always greater than the numerator. This relation shows the way that the In-between Root is shaved down from the Product Root when the Root Number is greater than one and is augmented when the Root Number is less than one. Those exponents act to temper the extremities of her brother, the Product Root. Also notice that the exponents of Hi and Lo are exactly reversed from step 11 to step 15.
While her brother, Prod, is a simple Product between the Parents, Hi and Lo, Mid is a complex product between the parents based upon roots. Notice how that a root is taken of a root in order to arrive at the In-between Root. This In-between Root is not a product or a sum or a difference. It is the Root of its Parents, who are themselves Roots. Its complexity is much greater than a simple product. This reminds of the idea that the position of awareness between subject and object is an increase in complexity, not just a mere blending. We have an example of an emergent phenomenon.
The first in-between theorems established the relations between the Kids, i.e. the In-between & Product Root, and their Genetics, i.e. the Root Number, and their Parents. The last theorem established the relationship between the In-between Root and her Parents, the Hi and Lo Roots. In this section we explore the relation between the In-between Root and the Root Number, L.
Step 16 is merely the 3rd In-between Theorem from above. In steps 17 and 18 we substitute the defined values for Hi and Lo into their respective expressions from equation 16. We then multiply through and simplify. In Step 18 we substitute these expressions back into equation 16.
This yields the relation we were looking for. It specifically shows the relation between the In-between Root, Mid, and the Root Number, L. It relates the Child with her Genetics.
Notice that the In-between Root is the Root of a product. This is a pretty stupid theorem because it follows immediately from our earlier explorations but it completes the cycle of family relations.
All of the above proofs have been standard algebra. Let us look at the same phenomenon in terms of our iterated General Root Functions.
>
We start in Equation 20 with our defined and derived F Series expression for the Hi Root. In Equation 21 we raise the Hi Root to the power it is in the Third In-between Theorem. Remember that this theorem shows how the Hi and Lo Root relate to the In-between Root. In Step 22 we merely substitute the expression for the Hi Root in equation 20 into the right hand side of Equation 21. This shows even more clearly how this expression is the root of a root.
Extending the same process to the Lo Root, we substitute the F Series expressions for the Hi and Lo Root into the formula for the In-between Root. This cumbersome expression is only meant to show the box within a box concept mentioned above. The Root of a Root.
Below are two other ways of expressing the In-between Root in terms of an iterative expansion. Equation 24 is the iterated expression for the 4th In-between Theorem, while Equation 25 is the iterated expression for the In-between Root that we established in the first section.