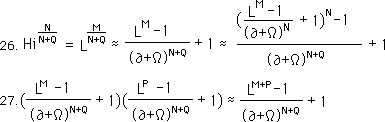
Home Science Page Data Stream Momentum Directionals Root Beings The Experiment
These different ways of expressing the In-between Root reveal some interesting properties of our Binomialized Root System.
Step 26 shows two ways of expressing the graded Hi Root, from equations 23 and 24. Step 27 shows the equality between the binomialized expressions in equations 24 and 25.
First it reveals that the exponents collapse in interesting ways. It only takes a simple proof to show the general case. In Step 28, we show a normal exponential identity. In Step 29, we simply rewrite this identity in Binomialized format.
We subtract one from both sides of the equation to get our first System theorem.
The normal question arises. What does this mean? This theorem shows that raising these binomialized expressions to a power is very different from usual. Normally we would have a complicated binomial expansion in the numerator. But in this case the N exponent in the numerator simply cancels out the N exponent of the top denominator, just as it does in step 28. More later.
Let us write this theorem in a simpler fashion. In this representation we substitute the Limit of the F Series expression for the binomial representation within the parenthesis and on the right side of the equation.
This second way of writing this theorem substitutes the F Series expression for the entire left side of the equation. This introduces a notation whereby the F Series expansion applies to the number within the parenthesis. With no parenthesis it is assumed that the number is the Root Number, L.
In this final representation of this theorem it is shown that the number within the parenthesis is not just L, but L to a fractional root.
Under the above circumstance, the exponents for the F Series can be treated like normal exponents, with the numerator of the one on the outside canceling the denominator on the inside.
In step 1 below we write another exponential identity.
Rewriting this in binomialized format is the 2nd System Theorem.
Again we have the unusual situation where an apparently complicated binomial expansion combines quite simply, just as in the first step.
As before let us write the second System Theorem in other forms. Below is the F Series representation for this 2nd Theorem.
Because the F Series expressions are the Limits of the series, we can expand the left side of the equation with normal algebra. We then subtract the ones, leaving us with the expression below.
This shows once again that the F Series product is not simple.
What are the implications of these Properties for the System of Iterated Rational Roots?
The immediate simplistic conclusion is that the exponents of these binomialized and F Series expressions can in no way be treated in normal exponential fashion. While the exponents of these iterative expressions have their own specifically defined properties, they are very different from the exponents of real numbers.
On looking at the differences a little more closely, one notices that the one that is added on to each expression is totally ignored in the transaction. While adding one to most expressions creates pandemonium, especially when raising these expressions to an exponent. In this case, in both theorems the one that is added on is ignored. The only expression that enters into the interaction is the F series component.
Similarly in both theorems the ‘-1’ component in the numerators of the equations is likewise ignored as if it weren’t even there. In the first theorem one of the ‘-1’s from the numerator disappears as if a ghost. In the second the confrontation between numerators evaporates because the ‘-1’ is treated as if it doesn’t exist.
Thus neither the ‘+1’ added on the general expression nor the ‘-1’ added to the numerator have any noticeable effect upon the above interactions. It is as if each operates primarily as an infinitesimal, able to avoid confrontation by not existing except as a concept. Let us see what happens when we treat these ones as infinitesimals in the above theorems.
Let us start by replacing all the ones in the Second System Theorem with our symbol for infinitesimal, a. This is shown in step 1 below. Subtracting or adding an infinitesimal to something real has no effect. This is shown in step 2, as most of the infinitesimals drop out.
Although most of the infinitesimals drop out, we have few rules to deal with the denominator. Certainly they do not behave like normal exponents, as is shown in the third expression of Step 2.
The question is how to evaluate this denominator, in our approximation process. We will call this denominator a Root generator. Simplistically, for this demonstration only, we will define its property as finding the root of the numerator as defined below.
The exponent of the denominator becomes the root of the numerator.
Using this substitution in Step 2 we get the desired result. Shown below in Step 3.
Thus when we treat the ones as infinitesimals and the denominator as a Root generator, our equations behave just like normal exponents. However let it be restated that the exponents in the denominator do not behave like normal exponents.
This same process is illustrated below for 2nd Theorem of the Process, dealing with exponentiation. In step 4 we substitute the infinitesimal for the ones. In Step 5 they drop out when subtracted or added to something real. In Step 6 our Root generator plays itself out yielding the desired answer.
Let us stress that the above approximations are just a way of understanding the process and the theorems it generates. The real equations are iterative processes that allow us to generate any rational root from any positive number and need the ‘+1’s, the ‘-1’s, and the Root generator as a customized binomial expansion to work. The above treatment is just a way of understanding how these customized processes work algebraically.
Simplistically our Infinite Continued Fraction Series, the F Series combines just like a normal number with a fractional root. If the ‘ones’ are treated as infinitesimals and the denominator like a root generator as described above, then the exponents for the binomialized expressions work like normal.
Let us dig a bit deeper. The ‘infinitesimal’ one that is first subtracted in the iterative process is then added back to whole after the iterative process stops. Let me repeat that the one is added after the iterations stop, not as part of the iterative process. Thus the F Series must be evaluated independently of the one that is added on and so exists as an independent entity.
Continuing to spew, while the F series must be evaluated independently of the one that is added, only when the one is added are the above Theorems valid, even though it is treated as an infinitesimal in the process. Thus as soon as the Root Generator (a+W)N appears in a fraction the number is transformed into an iterative expression whose limit ‘+ 1’ is some designated root. At that point the terms that form the entire expression that generates the root cease to exist independently. The parts of the expression are now a unit, which must be dealt with together.
As an example, the ‘+1’s are not part of the iterative process but are part of the exponential expression. Thus in any exponential process defined thus far, the ‘+1’ must be treated as part of the entire expression. This was shown in the two theorems just derived. However in any process that just involves adding and subtracting, multiplying and dividing, the ‘+1’ is to be treated as a separate algebraic entity.
On the other hand the ‘-1’s in the numerator are part of the iterative process. Thus they are totally linked to the iterative expression, the Root Generator. They can’t be treated as an independent algebraic numerator obeying the normal rules. They must be treated as part of the whole F Series expression.
Having sunk so deep, let us quickly take the grand perspective. From micro to macro. Let us see how the Infinite Continued Fraction Series, the F Series, fits into the concept of numbers. For context let us recreate a brief history of the development of numbers.
As humans we began with unitary, counting, whole numbers, which expressed discrete countable items. How many apples do we have? From here we progressed to adding groups of them. How many apples in the layer? This we called multiplication. Then we began adding groups of groups. How many layers of apples are in the crate, which results in how many apples? We even moved to the process of adding groups of groups of groups. How many crates of apples are in the warehouse, with how many layers of apples with all of their individual apples? This process we called exponentiation.
While we progressed quite far in this line of sophisticated counting, at one point we needed to divide some substances, which were not unitary, into parts. For instance we might have needed to divide a pie, if we were little, or a piece of property, if we were bigger. This led to fractional parts and the process of division of one whole number by another. While this simple process was never quite as exact as counting, it worked for most things pretty well. One pie divided into 4 parts. 9 acres of land divided into 5 parts. We could easily imagine that most everything could easily be numerated through whole numbers or fractions of whole numbers, i.e. the ratio of two whole numbers.
With these ratios we were also able to add, multiply, and exponentiate them, as well as divide them. While we could perform many operations with these fractions, we really wanted to know which one was larger. We humans always want the biggest piece. Was my 5 parts of 9 acres, more or less than your 4 parts of 7 acres? While there were complicated ways of deciding these issues, for instance breaking the acres into smaller countable pieces, the invention of the decimal system with its place holding zero was an incredible advance for simplicity. Any high school student and many elementary school students, as soon as they learn how to divide, can turn any fraction into a decimal for evaluation, to see if it is less or greater than some other fractional quantity. Understanding the relative value of fractions was enhanced in a major way by the decimal system.
While nearly everything could be broken into whole number ratios, we, as humans, found two things that weren’t able to be broken into a fraction. The first was the diagonal to a rectangle, which turned out to be one of our Roots. The second was the ratio of the circumference of a circle to its diameter, which we now call the transcendental number, Ļ. We obtained fractional approximations of these values fairly quickly, out of necessity.
While relative values of fractions are fairly easy to calculate manually, this is not true of the Root numbers. One could look at a fraction and turn it into a decimal through the process of division. However there is no simple process for evaluating Roots. Looking at a Root gives very little indication of its value except through guestimation, i.e. it’s probably about so and so. There is a complicated process for determining square roots, which no one knows, but there is no equivalent process for any of the higher fractional roots.
The values of fractions were exposed through the process of decimal division. These decimals could then easily be added, subtract, multiplied and divided. However this was not true of our Roots, which were called irrational numbers, because their decimals didn’t make any sense, had no order. (Not really. They were just not rational, ir-rational.) While we could put whole numbers and fractions into multiplication and additions, division and subtraction process, we could only put whole numbers into the exponents. As soon as fractions were put into exponents we had Roots and the problem of numerical evaluation.
A fraction has relatively immediate numerical meaning and can easily be manipulated. Our Roots just stand there with their roof over them. The student hopes it breaks into a recognizable entity. While recognizing it, it has no real meaning, except algebraic, with its roof over its head. This is where our F Series story begins.
In order to evaluate these numbers with roofs over their heads, our Roots, we set a variable plus one, ‘X+1’, equal to our Root, step 1 below. We raised both sides of our equation to the power of the Root. This turned our Root Number into a rational number, which we called L or a/b, step 2. The left hand side of the equation was raised to the power of the Root, ‘X+1’N, which resulted in a binomial expansion. At the beginning of every one of these expansions was XN and at the end was ‘+1’, step 3. A ‘-1’ was then added to both sides of the equation to negate this ‘+1’, step 4. Thus now on the left hand side of the equation we have LM -1, or (a/b)M -1, which turns into (a-b)M/bM, which we many times have called the constant c. This value is the numerator of our F series Formula.
On the left hand side of the equation a single x is factored out of the remaining elements, step 4. Both sides of the equation are then divided by the factor other than x, step 5. This leaves us with an iterative equation where x is a function of itself, x = f(x). This is an infinite continued fraction. For square roots the expression is complex for computation, for the higher roots the expression is prohibitive. The infinite continued fraction just represented a fancier hat, which yielded more understanding but little in terms of computational value.
From this point we derived F and D Series expressions for these infinite continued fractions. The F&D Series are both iterative expressions. With these iterative expressions we were able to express and compute any rational root simply. Below, in step 6, is the binomial expression that was used to express these iterative series. Notice that there is no difference between equation 5 and 6 except in the denominator. We have previously called this denominator the Root Generator.
X equals a fraction where the numerator is LM -1 and the denominator is the Root Generator. To understand what X means, we remember that X+1 equals the root, not just X. From this knowledge, step 1, we subtract one from both sides of the equation to find that X equals the Root minus one, step 7.
Setting the right side of equations 6 and 7 equal to each other we get step 8. We then add one to X’s iterative expression in order to bring it up to the appropriate Root.
Equation 9 expresses all rational roots as the Limit of an iterative process plus one. While ‘normal’, i.e. non-iterative, numbers cannot express irrational numbers, this iterative expression joins the irrationals and rationals into one family.
Notice that we subtract one from our iterative numerator while we add one to the iterative expression to make up the difference. Give and Take. The Balance.
In many ways, it is more appropriate to say that the Root - 1 = X or ń(į) rather than the Root = X-1. The reason is that the X expression is an iterative expression that needs to evaluated independently of the one that is added to it. This algebraic necessity needs to be constantly remembered when manipulating these ‘fractions’. In this sense equation 9 is a bit misleading unless one realizes that the iteration must be performed without the ‘+1’. Iterative algebra is different than traditional algebra because of the feedback effect.
What we are leading to is this. The ‘one’ that was added to the variable X, was something that allowed us to crack the Root in order to look inside. We opened it up with this infinitesimal crack that we subtracted away. But then we needed to add back what we subtracted away. We took a peek inside the Root with our ‘-1’ crack but then had to patch up our crack by adding back this same one. Thus the iterative process of subtracting the one infinitely from the numerator eventually adds up to one that is subtracted and so needs to be added back in.
For illustration of this concept of subtracting one and then adding it back in, let us begin another simplistic analysis, whose only merit is its ability to enable understanding, although it is itself incorrect. Let us begin with the general Root Formula.
Let us pretend that this is a ‘normal’ algebraic formula, when it is an iterative formula instead. In normal algebra we can break the fraction into two parts as is shown in step 2. Now we can analyze each part separately.
Because of the topic let us start with the middle expression. What does ‘-1’ over the Root Generator equal? This is shown in Step 3. We know that LM must equal zero for the numerator of the F series expression to equal -1, step 4. This is derived directly from the General Root Theorem, where the numerator equals LM - 1. If LM = 0 then L must equal zero, step 5, and immediately following comes the fact that our Root must also equal zero, LM /N= 0, step 6.
Going back to the Root Formula, we know that the Root - 1 equals this iterative expression as the number of iterations approaches infinity. This is expressed in step 7. Because the Root =0, we know that the iterative expression equals ‘-1’, just as we would have suspected.
Plugging these values back in equation 2, we get the expected result in Step 9. The -1 cancels out the +1 to yield 0. Further if we apply the Root Generator approximation that we used before, we arrive at the approximation that the Root equals the Root, as we would’ve hoped.
Backing up a little, we think, “If the ones cancel out, why not leave them out of the Root equation altogether. This would increase simplicity tremendously. The Root would just equal the LM divided by the Root Generator: none of those messy plus and minus ones to deal with.”
Unfortunately iterative equations do not obey standard algebraic procedure. In step 2 we ‘illegally’ broke apart an iterative expression for illustration only. The proof that the negative Root Generator equals ‘-1’ is true. However because the ‘-1’ is part of the iteration it cannot be separated out. The Root in no way equals this limited Root Generator expression. This is shown below in step 10. We stress this was just used for illustration and has no basis in actual iterative computation.
Let us reemphasize. Iterative expressions can’t be broken up or added onto without serious examination of the results. Iterative equations are like eco-systems where one change can throw everything off because of the constant repetitions of the process. It is impossible to break our iterative fraction into two parts. An iteration is just one event. It is integral, unitary, and can’t be divided up like that. There are no rules for breaking an iteration into two separate parts. On an even more trivial level, equations 1 and 2 are inaccurate because it is illegal to add a one to the iterative expression unless it is part of the process. That one should be subtracted from the Root rather than added to the iteration.
Thus while the iterated -1 in the numerator always equals -1 no matter what the root, it can in no way be broken out of the equation. Thus while this is an illustrative example of subtracting the one and then adding it back in, it cannot be broken into parts. We have a gestalt, a whole, which is indivisible without serious repercussions to the equality sign that separates the two parts. Another counter intuitive principle. The idea of breaking things into parts, which is so traditionally scientific, does not work with iterative expressions that are unitary.
One final topic that we will tackle clumsily is the primacy of the number one in the exponential system.
All of these ones, could it have been another number that was added to X, the original variable that we set equal to the Root? Not easily. Adding in zero, leaves us with an impregnable fortress of some radical Root with a number under it, X = LM/N. We can’t get inside anyway. Suppose we add in a two instead, X+2 = LM/N. Well first of all the number that will be subtracted from both sides will be 2 to the root power, not just one to the root power, which is always one. Second, the binomial expansion is complicated by the various powers of two, which are quite complicated compared to the powers of one, which always equal one. Thus adding one certainly is by far the simplest number to add to crack open our Root Radical simply because one to any power is still one.
While one is the simplest it is also the center of the exponential system. Any number greater than one that is raised to any positive exponent is always greater than one, which we’ve already proved. Further any number greater than one that is raised to a negative exponent, is always a positive number less than one. Any positive number less than one raised to a positive exponent always yields a positive number less than one. Any positive number less than one raised to a negative exponent always yields greater than one. One raised to any exponent always equals one. Thus one is the boundary between the positive numbers in the exponential scheme. Every positive rational number is stuck on its side of one whether greater than or less than one unless it encounters the reversal exponent, the negative exponent, in which case its relative location is reversed from less than one to greater than one or vice versa.
Below is a exponential graph that illustrates these points. It is set up to parallel a multiplication graph. For a normal Cartesian multiplication graph the point of origin is usually (0,0) while with our exponential graph it is (0,1). With multiplication, no matter how big or small, if the numbers are positive then the answer is also positive lying in the first Quadrant, the upper right. Similarly if the Root Number is greater than one and the exponent is greater than zero then the Root is also greater than one, no matter how large or small the Exponent or Root Numbers are. Similarly with the other quadrants. For instance the third quadrant is when the Root Number is less than one and the Exponent is less than zero then the Root is always greater than one, no matter how big or small the other numbers are within their limits.
There is only one thing ‘wrong’ with the parallels between the above graph and the Cartesian graph. Besides the fact of a different point of origin, the Root Number axis stops at zero. It never extends into the negative axis because this would entail the imaginary number system.
However by simply taking the logarithm of the Root Number and the Root, the parallel is complete. First when the Root Number is one its logarithm is zero which means that the point of origin for our logarithmic exponential graph is now (0,0) just like the Cartesian graph. Second, the Y-axis now extends upward towards positive like before, but now it also extends downward from zero to negative infinity. On the simplistic level it means that the four quadrants of our logarithmic exponential graph have exactly the same dimensions as the standard Cartesian graph.
Below is the logarithmic exponential graph with the identical quadrants as the Cartesian graph. Further, if the x-axis represents the exponent, T, and the y-axis equals the Logarithm of the Root Number, Log L, then the Log of will fall into the same quadrant as the Product of a multiplication table.
While, in and of itself, this exponential treatment is nothing new or unique, the reason that we bring it up at all is because of its intimate connection to our Infinite Continued Fraction Series, which is new and unique. What it shows is that the F Series values are in many ways a more accurate way of viewing Root Numbers than are their decimal equivalents. The decimal equivalents give no intimation of the primacy of the number one in exponential treatment. The F series, on the other hand only generates the difference between one and the Root. The one is only added on at the end. Further as we pointed out in our first Notebook on this topic, the F Series, which adds up to zero, is equivalent of the Root Number of One because of the one that is added as part of the Formula.
On a more complex level the logarithmic graph shows how the numbers between zero and one are identical with all the numbers greater than one. The infinite negative on the graph below is when our Root Number equals zero. The logarithm of zero is undefined because there is no number when multiplied times any other number that will yield zero, no matter how small.
As we showed in one of our earlier Notebooks, the numbers greater than one are an exact reflection of those positive numbers between one and zero. The numbers above one have a numerator greater than the denominator while the positive numbers less than one have a numerator who is less than the denominator. One is the only number whose numerator and denominator are the same. Therefore with our subtraction criterion for infinite numbers introduced in another paper, there is exactly the same amount of fractional numbers from 1 to infinity as there are from 0 to 1. This is not true of whole numbers. There are an infinite number of whole numbers greater than one while there are no whole numbers between 0 and 1.
For these reasons 1 is the zero of the positive exponential fractional Root Numbers. Therefore it makes perfect sense that our F series evaluations are in terms of its difference from one. The value of the iterative F Series is always equal to the Root plus one. If the Root Number is less than one then the F Series evaluation is always negative, while if the Root Number is greater than one then the F Series evaluation is always positive. Thus the primacy of the F Series in evaluating Roots is confirmed in the aspect that its numerical value is in relation to one not zero. Adding, subtracting, multiplying and dividing, even whole number exponentiation, always give numbers in relation to zero. Our F Series evaluation only gives results in relation to one. One must always be added on to turn it into the appropriate decimal. However as mentioned earlier the one has to be added after the iteration not during. Anyway we are amazed and bow down, humbly, quietly, before the glory and majesty of divinity.
One other topic of note, the graphs of the Root Beings only become a straight line when viewed from a logarithmic perspective. The intuitive feeling is that our Infinite Continued Fraction Series is properly meant to be viewed from this logarithmic perspective to turn it ‘normal’, i.e. linear. When we dealt with our Complex Spiral in a previous section of this paper, we dealt with this warping of space.
Now that we have examined the in-between fractional root in terms of the Binomialized F Series, let us take a step back and look at the implications. There are some parallels worth noting between the Mandelbrot set and our Root Beings.
Why have we spent so much time on these weird topics? We started by speaking about how the perimeter of the Mandelbrot set is organized. The perimeter is a continuous collection of larger and smaller bulbs. Each bulb is characterized by two whole numbers. One represents the period of the bulb, i.e. the number of limits in the orbit of the complex ‘c-value’ represented by the complex values inside the bulb. The other number represents how this period manifests, i.e. every other or every third or so forth. If the first number is the denominator and the second is the numerator, then each bulb can be assigned a fraction. The bulbs organize themselves numerically around the perimeter of the Mandelbrot set. Furthermore the fraction of the largest bulb between any two larger bulbs is always found by employing the Process described herein, i.e.. adding numerators and denominators of the fractions of the larger surrounding bulbs.
We found that not only were fractions organized this way, but that fractional roots of any number were also organized this way. The F Series as a representation of these fractional roots is also organized numerically by the System.
While this organization is merely a curiosity for rational roots and rational numbers, it reveals an underlying structure for the Mandelbrot set and the F Series. In the Mandelbrot set it determines the period of each bulb and the way it is manifested. In the F Series representation, the order of the denominator reveals the number of layers of feedback needed to generate this fractional root. If the denominator is squared then it means one level of feedback for the F Series or 2 layers of feedback for the D Series. If the Binomialized Denominator is raised to the 5th power, it means 4 layers of feedback for the F Series and 5 layers of feedback for the D Series. Therefore when two of the these fractional roots are combined it merely adds layers to the feedback. If a square root is combined with a fifth root, we get 7 layers of feedback for the resultant D Series. Thus the larger the denominator for both the F Series and Mandelbrot the higher the level of complexity. Repeating the denominator reveals the number of layers of feedback for the F Series while it reveals the period of the perimeter bulb in the Mandelbrot set .
Further the numerator for both the Mandelbrot set and the F Series has less of an impact on the complexity of the expression. In the Mandelbrot set it only indicates the manner in which the period manifests, while in the F Series it reveals a relative magnitude only, having nothing to do with the iterative process, except as a constant. Thus the numerator plays a subsidiary and dependent role to the denominator in both Mandelbrot and F Series representation.
Further we noticed that the In-between Root, manifested as a root of a root rather than being a multiplication or addition or some other process. The Parents of the In-between Root are both Roots. The In-between Root is a root of these roots. Its root is the sum of these roots. Thus all processes indicate an increase in complexity, not just magnitude. The In-between indicates an increase in cycle for the Mandelbrot set and an increase in the number of iterations for the F Series. In previous sections we even equated the increase in roots with an increase in negative dimensions. In summary the In-between Process indicates an increase in subtlety and complexity when applied to rational roots of the F Series and the periods of the Mandelbrot set. This is all we’ll say for now.
We’ve finally got the tools. Let’s open this baby up and see what’s inside. The baby in this case is the In-between F Series Root. Why do we care? First its context.
Basically we’ve got an F Series representation for rational roots whose organization mimics the Mandelbrot set in many key ways. The Process that organizes the Mandelbrot set also organizes the F Series. It organizes both fractions and fractional roots. It does this by generating In-between fractions. These In-between values are found by adding numerators and denominators of the surrounding fractions to find the in-between root. Besides being a way of easily organizing these systems from largest to smallest, this Process reflects the underlying structure of both systems. As such the F Series representation of the In-between Root is worth studying in its own right as it reflects much about the F Series System of Rational Roots.
The thrust of much of this section has been to find out what this In-between Root equals. Below is the F Series representation of the In-between Root, derived earlier.
We noticed that the Binomialized F Series of the In-between Root mimics the multiplication of two fractions with equal Root Numbers but with different exponents. While tempted to go this route, it was not true when exposed to greater examination. In other words this In-between Root was not a simple product of the Parent F Series’.
The Process, which is the sum of numerators and denominators of fractions, mimics the process of Exponentiation. However the exponent of the denominator is not the exponent of a real number, but is instead the exponent of an iterative process, which yields roots. While the denominators are indeed added to find the In-between Root, this is not what is going in terms of the multiplication of exponents. Fractions simply don’t work that way, even though this is the way it translates in the F Series.
The second System Theorem derived above showed how these fractional exponents combine in multiplication. Shown again below.
Indeed the numerators of fractional roots with like denominators do add together simply. However while the numerators add just like we want, the denominators, which are the same, remain the same. They do not double, multiply, add, or exponentiate; they just remain the same. This is not acceptable. The denominators as well as numerators must add. Repeating again, the product of two different F Series of the same Root Number do not combine simply, but must be treated like normal fractional exponents when added, i.e., common denominator and the like.
Repeating, multiplying the F Series with common denominators allows us to add the numerators like we want. But our F Series Parents have different denominators. Therefore we need some process that transforms our F series denominators into the same thing before the resultant F Series are multiplied. The process must not have an effect upon the numerator, because they are just like we want them. Just the denominators must be the same before the numerators are added.
What is this process? We will call it neutralization and transformation. This process is revealed by the System Theorem #1 above in combination with the In-between Root Theorem, which connects the Parents with the In-between Root. Let us reexamine the Theorems. First the In-between Root Theorem.
Now the System Theorem.
Basically in the In-between Process, as revealed in the In-between Root Theorem, the first thing that happens is that old roots are neutralized by inverse multiplication. After the neutralization or simultaneous with it the merged root is substituted. In other words the previous denominator doesn’t remain. Transcendence is complete. Emergence to a new level. Sometimes things become different by being added to, subtracted from, and multiplied by. In this case while the process mimicked multiplication, instead it was a process of neutralization and transformation. The old root is completely neutralized and completely replaced by the synthesis. Thus nothing of the old remains, only the synthesis. This is an emergent phenomenon where the synthesis transcends the parents.
The child will always have more layers of feedback than the parents for the F Series. Because of this the child, i.e. the In-between Root, belongs to a more complex dimension. Similarly the child bulb in the Mandelbrot set will always have more spokes, or limits, than the parent bulbs. This is not at all true with exponential multiplication, where the product might have the same denominator as its parents. Under certain circumstances the denominator of the product might even be less than the denominator of the parents. (Remember that the numerator of rational roots has nothing to do with its complexity.) This contrasts with the In-between Root, which is always more complex than its parents, i.e. has a larger denominator.
Remember that while the In-between Root is more complex that it is between its parents in size. It is never larger than both its parents. Further the In-between Child might be smaller or larger than with the Product Child of the Parents. Therefore size has nothing to do with the prestige of the In-between Root. The prestige of the In-between Root has to do with its increased complexity. It blends the complexity of its parents into a more complex and unique synthesis. Again nothing definitive can be said about the Product Child, which can be larger, smaller, less complex or more complex than its parents and the In-between Child. Thus the Product Child reveals little about the F Series System for fractional Roots.
Now that we have understood the In-between Root and its relations a little better, let us move onto the topic of patterned transcendentals, to increase our number family. We don’t know how this relates to anything that has been said so far. The Reader will have to plow ahead for a few more pages to find out.